Ridge와 Lasso로 과적합 제어하기 [ Linear Regression (선형회귀모델) 실습 ] [ 보스턴 데이터 ]

 

from sklearn.linear_model import Ridge

 

ridge모델명 = Ridge(alpha=?)

 

 

하이퍼 파라미터 alpha : 규제(= 제어, 정규화)의 정도를 의미한다.

 

해당모델에 똑같이 특성곱을 과하게 넣은 extended_X-_train을 넣고 fit으로 학습하고

 

 

 

alpha로 규제한 Ridge모델과 linear_model을 비교했을때 64 >> 77%로 올라감

 

 

 

 

이런식으로 alpha값에 따라 성능이 달라진다

 

 

Lasso :

 

Linear 모델이 MSE가 최소가 되게 하는 가중치화 절편을 찾았다면

Lasso는 여기에 가중치의 절대값의 합이 최소화되는 추가 제약조건이 있다.

즉 가중치의 값이 0이나, 0에 가깝게 되야함

 

MSE + 패널티 ( = a  * 요소의 절대값)

따라서 이 둘의 합이 최소가 되게 하는 w(가중치)와 b(절편)을 찾는것이 목적

MSE는 오차값이므로 작아질수록 Label과 예측값들의 차이가 작아지고

요소의 절대값이 작아질수록 w들이 0이 되거나 0에 가까워진다

 

알파가 커지면 패널티가 커지므로 요소의 절대값을 작게 만드는 것이 우선시되고

알파가 너무 작으면 MSE를 작아지게 하는것에 비중을 두게된다

Lasso는 w(가중치)가 0이 되게 함으로써 그에 해당하는 특성을 제외, 결과적으로 중요한 특성이 무엇인지 알게된다

 

 

Ridge : 

 

릿지는 라쏘와 거의 유사하나 라쏘와 다르게 가중치가 0에 가까워질뿐  0이 되진않는다

 

 

 

 

from sklearn.linear_model import  Lasso

 

lasso모델명 = Lasso(alpha=?)

.

 

 

 

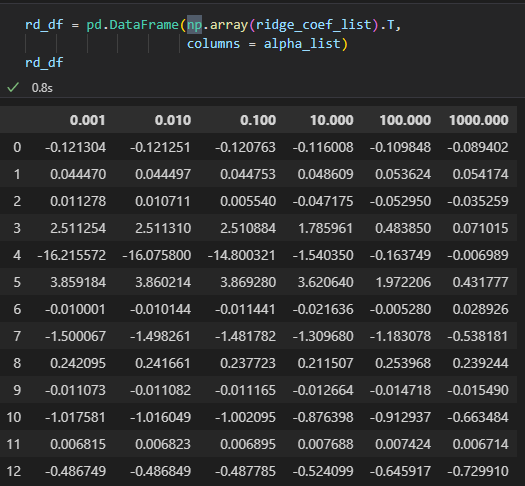
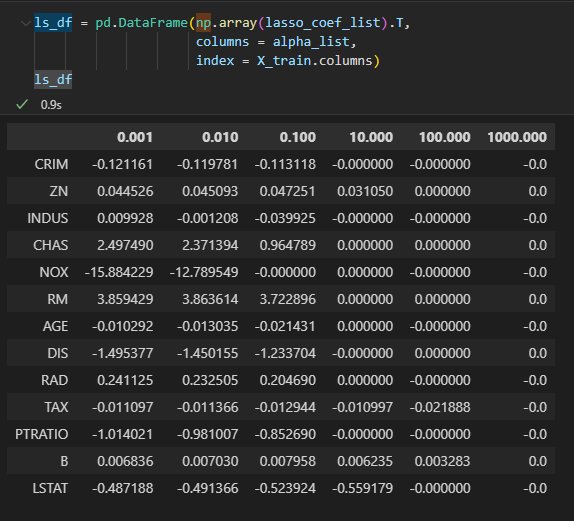
for문으로 alpha값에 따른 coef (기울기) = w 를 리스트에 담아 확인함

 

lasso는 0이 되지만 ridge는 0에 가까워질뿐 , 0이 되진않는 것이 확인됨